자료구조 & 알고리즘
[자료구조] Tree 순회 방법 - 전위/중위/후위 순회 & Java 예시 코드
토발자
2023. 8. 6. 23:38
반응형
자료 구조 중 트리가 있다.
트리 구조를 순회하는 방법에는 세 가지 방법이 있다.
- 전위 순회(Pre-order)
- 중위 순회(In-order)
- 후위 순회(Post-order)
이러한 순회 방법은 트리 내의 모든 노드를 방문하는 기초적인 방법들로서, 트리 구조를 다루는데 중요한 역할을 한다.
순회 방법은 트리의 형태와 원하는 결과에 따라 다르게 선택될 수 있다.
그렇다면 이 3가지 트리 순회에 대해 알아보자.
전위순회(Pre-order)
전위순회는 다음 순서로 노드를 순회한다.
Root - Left - Right
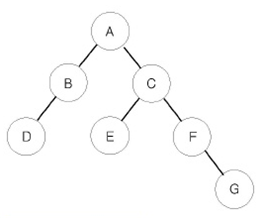
상단의 트리를 전위순회로 순회한다면 다음과 같은 순서로 노드를 순회할 것이다.
- 전위 순회한 결과 : ABDCEFG
중위순회(In-order)
중위순회는 다음 순서로 노드를 순회한다.
Left - Root - Right
- 중위 순회한 결과 : DBAECFG
후위순회(Post-order)
후위순회는 다음 순서로 노드를 순회한다.
Left - Right - Root
- 후위 순회한 결과 : DBEGFCA
각각의 순회 방식에 대해 Root의 위치로 기억하면 편할 것 같다.
트리를 순회하는 방법은 주로 재귀적으로 구현된다.
재귀를 통해 트리의 노드를 방문하면서 순회를 수행할 수 있다.
또한, 스택(Stack)이나 큐(Queue)를 이용하여 반복적으로 순회할 수도 있다.
트리 순회 Java 예시 코드
아래는 각각의 순회 방법에 대한 Java 예시 코드다.
아래의 예시 코드는 이진 트리(Binary Tree)를 기준으로 작성되었다.
우선 이진 트리의 노드를 나타내는 클래스를 정의한다.
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}
전위순회
void preOrderTraversal(TreeNode root) {
if (root == null) return;
// 루트 노드를 방문
System.out.print(root.val + " ");
// 왼쪽 서브트리를 전위 순회
preOrderTraversal(root.left);
// 오른쪽 서브트리를 전위 순회
preOrderTraversal(root.right);
}
중위순회
void inOrderTraversal(TreeNode root) {
if (root == null) return;
// 왼쪽 서브트리를 중위 순회
inOrderTraversal(root.left);
// 루트 노드를 방문
System.out.print(root.val + " ");
// 오른쪽 서브트리를 중위 순회
inOrderTraversal(root.right);
}
후위순회
void postOrderTraversal(TreeNode root) {
if (root == null) return;
// 왼쪽 서브트리를 후위 순회
postOrderTraversal(root.left);
// 오른쪽 서브트리를 후위 순회
postOrderTraversal(root.right);
// 루트 노드를 방문
System.out.print(root.val + " ");
}
이 코드를 기반으로 트리를 생성하고 전위 순회, 중위 순회, 후위 순회를 수행하여 결과값을 출력해보자.
이진트리는 다음과 같다.
1
/ \
2 3
/ \
4 5
이진 트리의 각 노드는 1부터 5까지의 값을 가진다.
이진 트리의 노드를 생성하고 연결해 전위 순회, 중위 순회, 후위 순회를 수행한 결과를 출력해보면 다음과 같다.
public class Main {
public static void main(String[] args) {
// 이진 트리 생성
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
// 전위 순회 출력
System.out.print("Pre-order Traversal: ");
preOrderTraversal(root);
System.out.println();
// 중위 순회 출력
System.out.print("In-order Traversal: ");
inOrderTraversal(root);
System.out.println();
// 후위 순회 출력
System.out.print("Post-order Traversal: ");
postOrderTraversal(root);
System.out.println();
}
}
/* 출력 결과
Pre-order Traversal: 1 2 4 5 3
In-order Traversal: 4 2 5 1 3
Post-order Traversal: 4 5 2 3 1
*/
반응형