반응형
자료구조 중 트리(Tree)에 대해 정리해보자.
트리(Tree)란?
트리(Tree)는 계층적인 구조를 나타내는 비선형 자료구조로 그래프(Graph)의 특수한 형태이다.
트리는 노드(Node)와 간선(Edge)으로 이루어져 있다.
간단히 말해 트리는 하나의 루트 노드를 가지고 있으며, 각 노드는 0개 이상의 자식 노드를 가질 수 있다. 이러한 구조로 인해 데이터를 계층적으로 표현할 수 있다.
트리의 주요 개념과 용어는 다음과 같다.
- 노드(Node) : 트리의 기본 단위로 데이터를 저장하는 요소다. 각 노드는 부모 노드와 하위 노드(자식 노드)를 가질 수 있다.
- 루트(Root) : 트리의 맨 위에 있는 노드로 다른 모든 노드는 루트를 향해 이어진 경로를 가지고 있다. 트리는 하나의 루트 노드만을 가진다.
- 부모(Parent)와 자식(Child) : 다른 하나 이상의 노드(자식 노드)를 가리키는 노드다. 자식 노드는 그 부모 노드에 의해 생성된다.
- 조상(Ancestor)과 자손(Descendant) : 조상은 특정 노드에서 루트까지 이어지는 경로 상의 모든 노드를 말하며, 자손은 특정 노드에서 아래쪽으로 이어지는 모든 노드를 말한다.
- 형제(Sibling) : 같은 부모 노드를 가진 자식 노드들을 말한다.
- 잎(Leaf) 노드 : 자식 노드를 가지지 않는 노드로 트리의 가장 하위에 위치한다.
- 서브트리(Subtree) : 트리에서 특정 노드와 그 하위 자손들로 이루어진 부분 트리를 말한다. 모든 노드는 하나의 서브트리다.
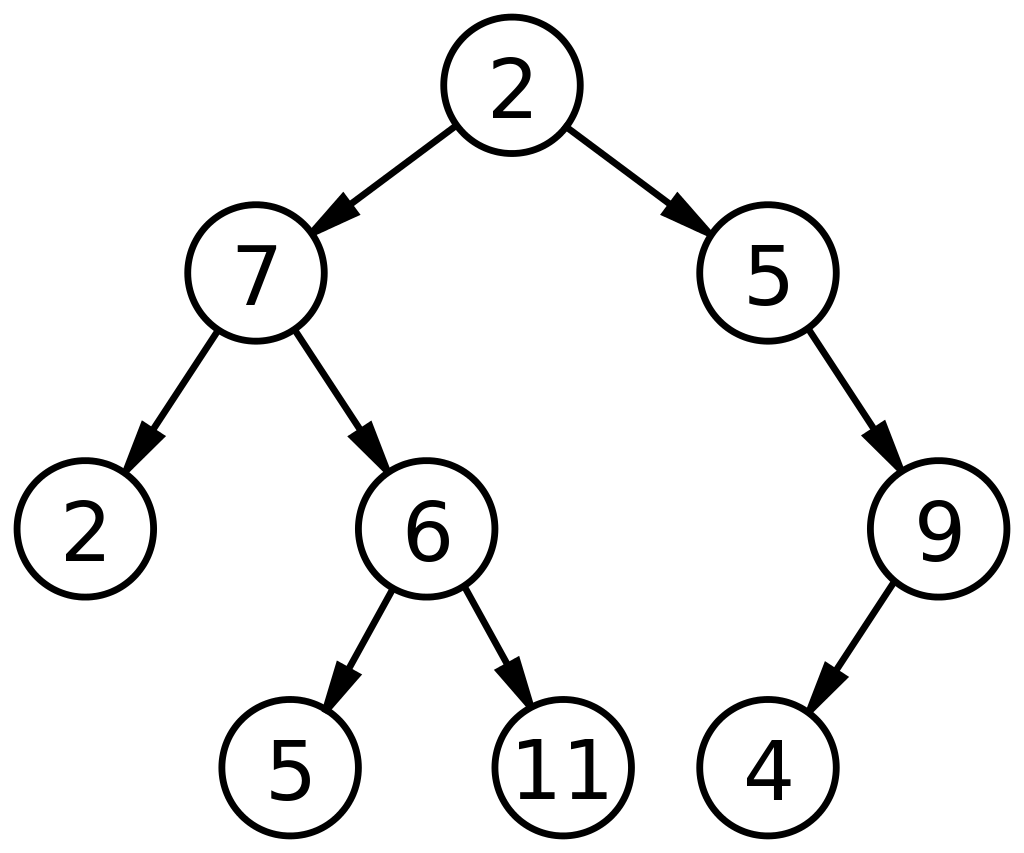
트리(Tree)의 장점 및 단점
장점
- 계층적 구조 : 트리는 계층적인 구조를 가지고 있어 데이터를 계층적으로 표현할 수 있다. 이로 인해 트리는 현실 세계의 많은 문제를 효과적으로 모델링할 수 있다.
- 빠른 탐색 속도 : 이진 탐색 트리(Binary Search Tree)의 경우 데이터를 정렬된 상태로 유지하므로 탐색, 삽입, 삭제 연산에 대해 평균적으로 O(log n)의 시간 복잡도를 가진다.
- 자기 참조적 구조 : 트리는 자기 참조적인 구조를 가지고 있어 특정 노드에서 서브트리 전체를 나타내거나 탐색할 수 있다. 이를 활용하여 효율적인 재귀 알고리즘을 구현할 수 있다.
- 정렬 및 범위 검색 : 이진 탐색 트리와 같은 정렬된 트리 구조는 정렬된 상태를 유지하므로 범위 검색에 유리하다. 정렬된 순서로 데이터에 접근할 수 있어 효율적인 검색이 가능하다.
단점
- 삽입 및 삭제의 복잡성 : 트리의 구조를 유지하기 위해 삽입 및 삭제 연산이 복잡할 수 있다. 특히, 불균형한 트리의 경우 트리의 재조정이 필요할 수 있어 추가적인 연산이 필요하다.
- 메모리 사용 : 트리는 포인터로 연결된 노드 구조를 가지고 있기 때문에 메모리 사용이 비교적 크다. 트리의 균형을 유지하기 위해 추가적인 포인터를 사용하는 경우 메모리 사용이 더욱 증가할 수 있다.
- 순회 순서의 의존성 : 트리의 순회 순서는 트리의 구성에 따라 달라진다. 따라서 트리에 저장된 데이터를 순차적으로 접근해야 하는 경우 순회 순서에 따라 접근해야 하므로 일반적인 순차 자료구조보다는 조금 더 복잡할 수 있다.
Tree 예시 코드(Java)
다음은 Java에서 사용하는 Tree의 레퍼런스 코드다. 이 코드는 이진 트리(Binary Tree)를 예로 들었다.
이진트리란 자식노드가 최대 2개인 노드로 구성된 트리다. 즉, 부모 노드로부터 자식 노드가 0~2개 사이로 존재할 수 있다.
class TreeNode {
private int data;
private TreeNode left;
private TreeNode right;
public TreeNode(int data) {
this.data = data;
this.left = null;
this.right = null;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public TreeNode getLeft() {
return left;
}
public void setLeft(TreeNode left) {
this.left = left;
}
public TreeNode getRight() {
return right;
}
public void setRight(TreeNode right) {
this.right = right;
}
}
class BinaryTree {
private TreeNode root;
public BinaryTree() {
root = null; // 이진 트리의 루트 노드 초기화
}
public boolean isEmpty() {
return root == null; // 이진 트리가 비어 있는지 여부 반환
}
public void insert(int data) {
root = insertNode(root, data); // 데이터를 이진 트리에 삽입
}
private TreeNode insertNode(TreeNode current, int data) {
if (current == null) {
current = new TreeNode(data); // 현재 노드가 null인 경우 새로운 노드 생성
} else {
if (data <= current.getData()) {
current.setLeft(insertNode(current.getLeft(), data)); // 데이터가 현재 노드의 데이터보다 작거나 같으면 왼쪽 자식에 삽입
} else {
current.setRight(insertNode(current.getRight(), data)); // 데이터가 현재 노드의 데이터보다 크면 오른쪽 자식에 삽입
}
}
return current;
}
public boolean search(int data) {
return searchNode(root, data); // 데이터를 이진 트리에서 검색
}
private boolean searchNode(TreeNode current, int data) {
if (current == null) {
return false; // 현재 노드가 null인 경우 데이터를 찾지 못한 것이므로 false를 반환.
}
if (data == current.getData()) {
return true; // 현재 노드의 데이터와 찾는 데이터가 일치하면 true를 반환
} else if (data < current.getData()) {
return searchNode(current.getLeft(), data); // 데이터가 현재 노드의 데이터보다 작으면 왼쪽 자식을 탐색
} else {
return searchNode(current.getRight(), data); // 데이터가 현재 노드의 데이터보다 크면 오른쪽 자식을 탐색
}
}
public void delete(int data) {
root = deleteNode(root, data); // 데이터를 이진 트리에서 삭제
}
private TreeNode deleteNode(TreeNode current, int data) {
if (current == null) {
return null; // 현재 노드가 null인 경우 삭제할 데이터를 찾지 못한 것이므로 null 반환
}
if (data == current.getData()) {
// 삭제할 노드가 단말 노드인 경우
if (current.getLeft() == null && current.getRight() == null) {
return null; // 왼쪽과 오른쪽 자식이 없는 단말 노드를 삭제하고 null 반환
}
// 삭제할 노드가 오른쪽 자식만 가지는 경우
else if (current.getLeft() == null) {
return current.getRight(); // 오른쪽 자식을 현재 노드로 대체
// 삭제할 노드가 왼쪽 자식만 가지는 경우
else if (current.getRight() == null) {
return current.getLeft(); // 왼쪽 자식을 현재 노드로 대체
}
// 삭제할 노드가 양쪽 자식을 가지는 경우
else {
int smallestValue = findSmallestValue(current.getRight()); // 오른쪽 서브트리에서 가장 작은 값을 찾는다
current.setData(smallestValue); // 삭제할 노드의 데이터를 찾은 가장 작은 값으로 대체
current.setRight(deleteNode(current.getRight(), smallestValue)); // 가장 작은 값을 가진 노드를 삭제
return current;
}
} else if (data < current.getData()) {
current.setLeft(deleteNode(current.getLeft(), data)); // 데이터가 현재 노드의 데이터보다 작으면 왼쪽 자식 삭제
return current;
} else {
current.setRight(deleteNode(current.getRight(), data)); // 데이터가 현재 노드의 데이터보다 크면 오른쪽 자식 삭제
return current;
}
}
private int findSmallestValue(TreeNode root) {
// 오른쪽 서브트리에서 가장 작은 값을 찾기 위해 왼쪽 자식으로 계속 이동한다.
return root.getLeft() == null ? root.getData() : findSmallestValue(root.getLeft());
}
}
위의 코드에서 TreeNode 클래스는 트리의 각 노드를 나타내며, BinaryTree 클래스는 이진 트리를 관리하는 메서드들을 제공한다. 이 코드를 사용해 이진 트리를 생성하고, 데이터를 삽입, 검색, 삭제할 수 있다.
반응형
'자료구조 & 알고리즘' 카테고리의 다른 글
| [Algorithm] Big-O 표기법이란(+ 시간 복잡도, 공간 복잡도) (0) | 2023.06.13 |
|---|---|
| [자료구조] 해시 테이블(Hash Table) 자료구조 알아보기 & Java 예제 코드 (0) | 2023.06.11 |
| [자료구조] 그래프(Graph) 자료구조 알아보기 & Java 예제 코드 (0) | 2023.06.10 |
| [자료구조] 힙(Heap) 자료구조 알아보기 & Java 예제 코드 (0) | 2023.06.10 |
| [자료구조] 큐(Queue) 자료구조 알아보기 & Java 예제 코드 (0) | 2023.06.06 |
