우선순위 큐(Priority Queue)와 힙(Heap)에 대해 간단히 알아보자.
우선순위 큐(Priority Queue)란?
- 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조이다.
- 어떤 데이터를 우선순위에 따라 처리하고 싶을 때 사용한다.
- ex) 상품 데이터를 자료구조에 넣었다가 비싼(가치가 높은) 상품부터 꺼내서 조회할 경우 : 이 때 상품의 가치를 상품과 함께 저장해 추출 시 가치가 높은 상품부터 꺼내도록 한다.
여기서 다시 한 번 스택(Stack), 큐(Queue), 우선순위 큐(Priority Queue) 자료구조를 비교/정리해보고 가자.
| 자료구조 | 가장 먼저 추출되는 데이터 |
| 스택(Stack) | 가장 나중에 삽입된 데이터(후입선출) |
| 큐(Queue) | 가장 먼저 삽입된 데이터(선입선출) |
| 우선순위 큐(Priority Queue) | 가장 우선순위가 높은 데이터 |
우선순위 큐(Priority Queue)의 구현 방법
- 우선순위 큐(Priority Queue)의 구현 방법 중 대표적으로 2가지가 있다.
1️⃣ 리스트(List)를 이용한 구현 : 리스트에 데이터를 넣은 뒤에, 데이터를 꺼낼 때 리스트에서 확인 후 가치가 큰 것을 뽑아서 추출한다.
2️⃣ 힙(Heap)을 이용한 구현 : 아래에서 힙(Heap)을 이용한 구현 방법에 대해 자세히 설명할 예정이다.
- 데이터 개수가 N개일 때, 구현 방식에 따라 시간 복잡도를 비교하면 다음과 같다.
- 리스트(List) 데이터 삽입 시에는 단순히 데이터를 뒷 쪽에 연달아 넣으면 되기 때문에 시간 복잡도는 O(1)이다.
- 리스트(List)를 이용해 우선순위 큐에 담긴 데이터를 삭제할 때의 시간 복잡도는 O(N)이다. 삭제하고자 하는 데이터는 가장 우선순위가 높은 데이터로, 이 데이터를 찾기 위해 선형적인 탐색시간이 소요되기 때문이다.
- 힙(Heap)의 경우 데이터를 삽입과 삭제 모두 최악의 경우에도 O(logN) 시간 복잡도를 보장하는 방식으로 동작한다.
- 힙 정렬 : 힙(Heap) 같은 경우 데이터의 삽입과 삭제에 있어서 O(logN)의 시간이 소요되기 때문에 단순히 N개의 데이터를 힙에 넣었다가 모두 꺼내는 작업만 수행하더라도 그 자체로서 정렬이 수행된다는 점이 특징이다.
- 이 때, N개의 데이터를 모두 힙에 넣기 위해서 O(NlogN)의 시간 복잡도가 소요되고, N개의 데이터를 힙에서 꺼낼 때도 마찬가지로 O(NlogN)의 시간 복잡도가 소요된다.
- O(NlogN)의 시간 복잡도를 가지고 있어 다른 정렬 알고리즘과 동일하게 빠른 알고리즘이라고 볼 수 있다.
| 우선순위 큐 구현 방식 | 데이터 삽입 시간 | 데이터 삭제 시간 |
| 리스트(List) | O(1) | O(N) |
| 힙(Heap) | O(logN) | O(logN) |
그렇다면 실제로 힙(Heap) 자료구조는 어떻게 구현할 수 있을지 살펴보자.
힙(Heap)의 특징
- 힙(Heap)은 완전 이진 트리(Complete Binary Tree) 자료구조의 일종이다.
- 힙(Heap)에서는 항상 루트 노드(root node)를 제거한다.
- 데이터를 넣을 때는 트리에 넣고, 데이터를 꺼낼 때는 루트 노드에 위치한 데이터가 나오도록 한다.
- 힙(Heap)의 2가지 분류
1️⃣ 최소 힙(Min Heap)
- 루트 노드가 가장 작은 값을 가진다.
- 값이 작은 데이터가 가장 먼저 제거된다.(= 오름차순)
- 아래 그림에서 루트 노드인 6인 전체 트리에서 가장 작은 값을 갖고 있다. 7이 적힌 노드를 보면 서브트리에서 가장 작은 값을 갖고 있는 것을 볼 수 있다.

2️⃣ 최대 힙(Max Heap)
- 루트 노드가 가장 큰 값을 가진다.
- 값이 가장 큰 데이터가 우선적으로 제거된다.(= 내림차순)

완전 이진 트리(Complete Binary Tree)
- 루트(root) 노드부터 시작해 왼쪽 자식 노드, 오른쪽 자식 노드 순서대로 데이터가 차례로 삽입되는 트리를 의미한다.
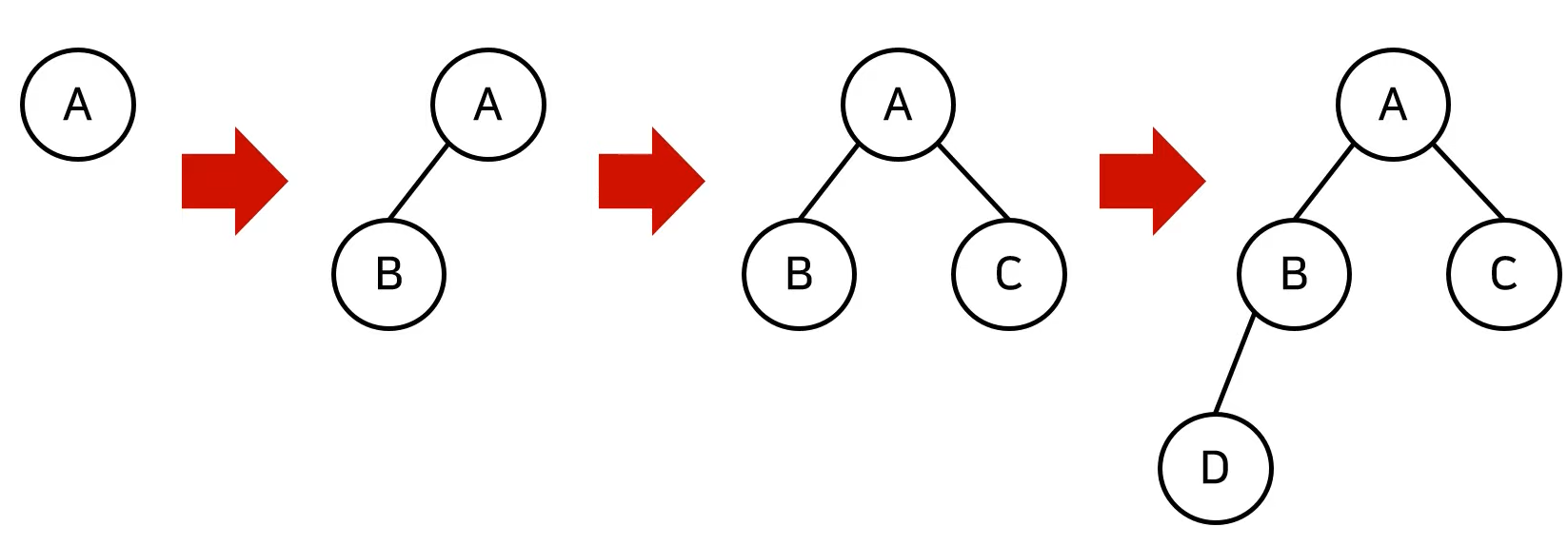
그렇다면 어떤 데이터를 힙(Heap)에 넣었을 때 해당 힙이 힙(Heap)의 자료구조 성질을 갖게 하려면 어떻게 해야 할까?
최소 힙 구성 함수 : Min-Heapify()
1. heap에 새로운 원소가 삽입될 때
- 일반적으로 heap을 구성하기 위한 함수의 이름을 heapify()라고 한다.
- heapify()는 상향식과 하향식으로 구현 가능하다. 여기서는 상향식을 알아본다.
- 상향식 heapify : 부모 노드로 거슬러 올라가며, 부모보다 자신의 값이 더 작은 경우에 위치를 교체한다.
- 새로운 데이터 5가 들어옴
- 1번 서브 트리는 최소 힙 성질을 만족하지 않는 서브 트리이다.
- heapify() 함수로 1번 서브트리에서 최소 힙 조건을 만족한다면 상위의 부모와 값을 비교해 자신의 값이 더 작다면 또 다시 위치를 교체한다.
- 2번을 확인하면 삽입된 데이터 5가 루트 노드로 위치가 변경된 것을 볼 수 있다.

- 힙(Heap)은 완전 이진 트리를 따르기 때문에 균형 잡힌 트리로서 동작한다.
- 따라서 부모 노드 쪽으로 거슬러 올라가거나 부모 노드에서 자식 노드로 내려올 때 최악의 경우에도 O(logN)의 시간 복잡도를 보장한다.
- 위의 경우를 보면 삽입된 데이터 5는 12와 6, 단 2번만 거슬러 올라가도 루트까지 도달한다.
- 이처럼 전체 데이터 개수가 N개일 때 logN의 시간 복잡도로 루트까지 heapify 함수를 이용해 각 데이터들을 확인 가능하다.
2. heap에서 원소가 제거될 때
- 마찬가지로 원소가 제거되었을 때도 O(logN)의 시간 복잡도로 힙(Heap) 성질을 유지하도록 할 수 있다.
- 앞서 설명했듯 힙(Heap)에서는 항상 루트 노드(root node)를 제거한다.
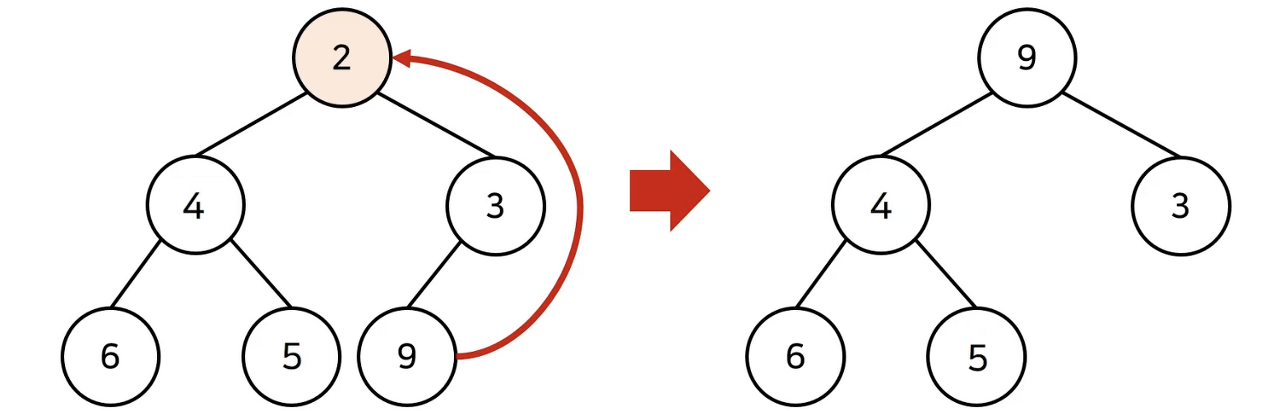
- 원소를 제거할 때의 순서를 살펴보면 다음과 같다.
- 가장 마지막 노드가 루트 노드의 위치에 오도록 한다.
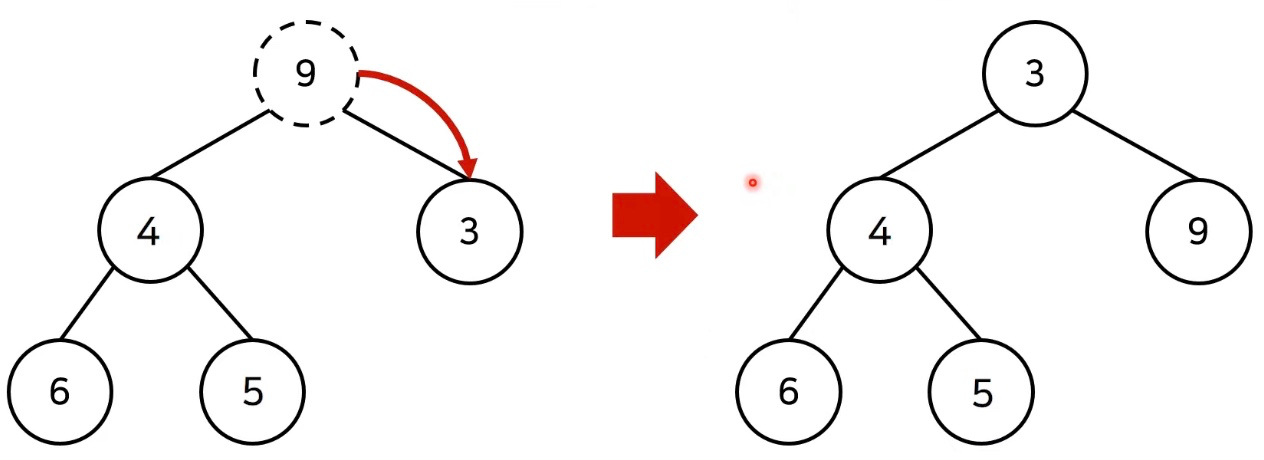
- 이후에 루트 노드에서부터 하향식으로(더 작은 자식 노드로) heapify()를 진행한다.
- 하향식 heapify는 상향식과 반대로 자식 노드를 확인해서 더 값이 작은 자식과 루트 위치를 바꾼다.
마지막으로 각 프로그래밍 언어마다 기본적으로 제공하는 Heap 라이브러리가 있다.
이 라이브러리가 최소 힙인지, 최대 힙인지는 다르다.
예를 들면 Java, Python의 우선순위 큐 라이브러리는 가치가 낮은 것에 우선순위가 있는 최소 힙 형태로 동작한다.
출처 : 동빈나 유튜브 - https://www.youtube.com/watch?v=AjFlp951nz0)
'자료구조 & 알고리즘' 카테고리의 다른 글
| [자료구조] 연결 리스트(LinkedList) 자료구조 알아보기 & Java 예제 코드 (0) | 2023.06.04 |
|---|---|
| [자료구조] 배열(Array) 자료구조 알아보기 & Java 예제 코드(+ ArrayList) (0) | 2023.06.04 |
| [백준] 10828 스택 자바 문제 풀이(시간 초과 해결) (0) | 2022.07.24 |
| [기초 자료구조] Stack(스택) - Array 기반 / LinkedList 기반 (0) | 2022.07.24 |
| [JAVA] Java Collections Framework(자바 컬렉션 프레임워크) (0) | 2022.07.24 |
